شرح درس الرياضيات التوازي و التعامد السادس ابتدائي

درس التوازي و التعامد السادس ابتدائي

تقديم 

مدونتكم مدونة معرفة تقدم لكم شروحات لدروس لمختلف المواد الدراسية ،رغبة منا في مزيد من الفهم و التفوق.

في درسنا اليوم سنتطرق لشرح درس الرياضيات التوازي و التعامد السنة السادسة ابتدائي، وكنحاول توضيح مختلف الخصائص المحددة للتوازي و التعامد ، كما سنطرح بعض التمارين مع حلولها لكي يكون التوضيح تطبيقيا.

التوازي 

نقول عن مستقيمان متوازيان اذا كانا :

• متطابقان تماما مثال: 

 المستقيمان D1 و D2 متطابقان اذن هما متوازيان، نقرأ (D1) يوازي (D2), و نكتب  (D1)//(D2) .

• مستقيمان لا يتقاطعان ابدا  مثال : 
  

المستقيمان (D1) و (D2) لا يتقاطعان ابدا مهما تم تطويلهما ، اذن فإنهما متوازيان، نقرأ (D1) يوازي (D2) و نكتب (D1)//(D2).

التعامد 

يكون مستقيمان متعامدان اذا كانا يتقاطعان ليكونا زاوية قائمة .

المستقيمان (D1) و (D2) يتقاطعان مكونات زاوية قائمة اذن فهما مستقيمان متعامدان .

نقرأ (D1) عمودي على (D2) او العكس ، و نكتب :

خصائص التوازي و التعامد

• اذا كان مستقيمان متوازيان فكل مستقيم مواز لأحدهما فهو مواز الآخر .

لدينا D1 و D2 متوازيان ، و D3 يوازي D2 و بالتالي فإن D3 يوازي D1 

• اذا كان مستقيمان متوازيان فكل مستقيم عمودي على أحدهما فهو عمودي على الآخر .
  
  D1 يوازي D2 , و D3 عمودي على D1 ,اذن فإن D3 عمودي على D2 .
• اذا كان مستقيمان متعامدان فإن كل مستقيم عمودي على أحدهما فهو موازي للآخر.
  
  
  
• اذا كان مستقيمان متعامدان فكل مستقيم موازي لأحدهما فهو عمودي على الآخر .

تمرين تطبيقي 

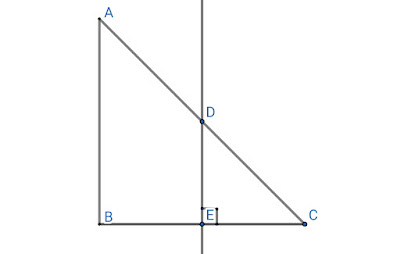
ليكن المثلث ABC القائم الزاوية في الرأس B , ليكن النقطة D من الضلع AC .

1- ارسم المستقيم المار من D  و الموازي للمستقيم AB ، و يقطع BC في النقطة E .

2- كيف هما المستقيمان DE و BC .

3- ارسم المستقيم العمودي على AB في النقطة F و المار من المستقيم AC في النقطة G .

4- كيف هما المستقيمان FG و BC .

الحل: 

1-

2-لدينا المثلث قائم الزاوية في B اذن فإن AB هو عمودي على BC ،و بما أن DE هو موازي ل AB فإن DE هو عمودي على BC في É

3- 

4- لدينا المستقيمان AB و BC متعامدان ، اذن بما أن FG هو عمودي على AB فإن FG// BC .

تمارين في الدرس